Professor of the Institute of Engineering and Technology, Associate Professor of the School of Economics and Management of South Ural State University, Doctor of Sciences (Engineering) Sergei Aliukov published a paper in the journal of Mathematics (TOP-10 Web of Science; Q1 Scopus), where he proposed a new approach to macroeconomics modelling.
Microeconomics studies the processes at the level of companies and corporations, while macroeconomics – at the level of countries. Simply put, it seeks to answer the question why some countries are rich and others are poor, and why the economy in some countries grows faster, and in others – slower.
There is a classical model, which is mentioned in today’s text books for students – the Solow model, for which its author, Robert Solow, was awarded the Nobel Prize. Based on differential equations, it shows how in a closed economy (without consideration to international connections) the production function grows, and together with it – both the gross national project and the whole economy do.
This model was created in the mid 1950s, when the classical mathematical analysis reigned in applied sciences. Researchers believed that it would be better to build a theoretical model with continuous or even smooth functions. There is no such thing in real life of course, but in case of specific computations we could try and “adapt” life to theory.
In the 21st century, we hear more and more calls for the need of new models. A bigger and bigger role in the world economy is being played by the countries of the “Global South”, the so called “developing countries”. And one cannot imagine their development without gaps, surges and bifurcations – that is, all those events unforeseen by the theory, for which Nassim Taleb coined a black swan term once.
In other words, we are talking about those “quickly changing” processes, which are quite normal now for the modern economy of countries.
It is difficult to adapt reality to a classical model (for instance, using Fourier's series) due to the Gibbs effect: even a single burst – black swan’s flap – would taint the big picture.
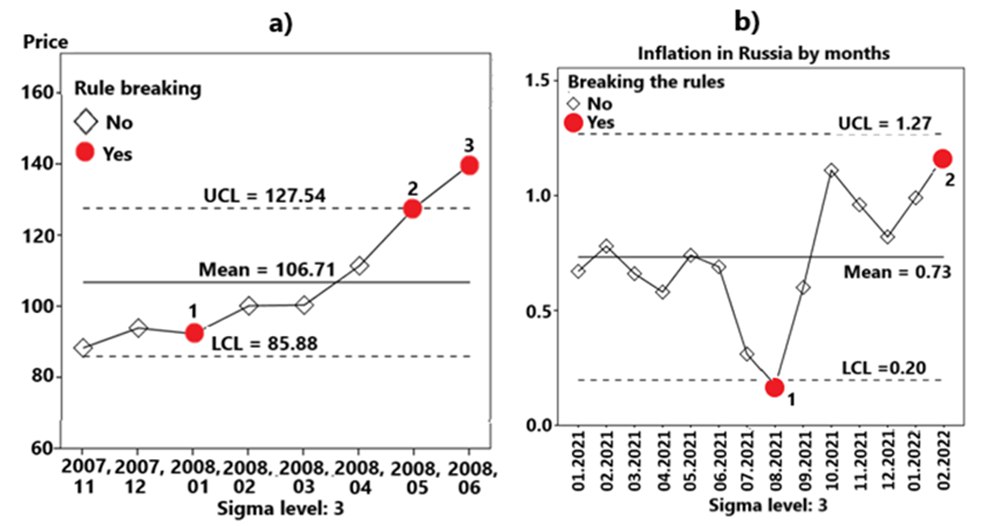
Examples of building forecasts for the Russian rouble inflation (to the right) and for Brent crude oil prices (to the left)
Sergei Aliukov is an approximation theory expert. Recently, in Russia, he has published a monograph on function approximation, and a text book is planned to be released by the Elsevier international publishing house.
Many people would most likely be familiar with the term of approximation as it is similar to the Latin or English word “approximate” meaning “in round figures”. Indeed, the primary task of approximations is to help transform real data into functions, which classical models are ready to work with. Usually this is achieved through piecewise linear functions (imagine a jogged line roughly imitating the run of a smooth curve). To take the unforeseen-for “black swans” into account, such functions are complimented with jumps and the so-called generalised functions.
In his work, Sergei Aliukov described the main types of the “special features” (steps, jumps, shifts, shocks, and impulses) and learned how to use them to build approximations for functions so that the Gibbs effect, that distorts the final result in case of jumps, would not hamper the process.
Next, in his paper, Professor Aliukov proposed a selection of the crucial macroeconomical parameters: 15 main and 7 supplementary ones. Namely these parameters would determine the economic growth in this case. They include the level of GDP growth per capita, unemployment rate, employability age for males and females, inflation rate, balance of trade, national debt in the percent of GDP, consumer price index, corporation tax rate, and other parameters. For correct application of this model, one should collect these parameters in a continuous manner (ideally, on a daily basis, but within a long period of time – then the scale becomes bigger).
Traditionally, students are taught to compare the economic indicators by pairs – calculate their correlation ratio and build an econometric (regressional) dependence. In the model by Sergei Aliukov, thanks to the cluster analysis, factor analysis and multidimensional scaling methods, it becomes possible to identify the dependence between several parameters simultaneously.
The model aims at building a forecast of the macroeconomic growth. Many market researchers, even without immersion into mathematics, know of the Six Sigma rule. Sigma is an example of a mathematical concept which made its way to every day speech. In mathematics this letter is used to demote a root-mean-square deviation, which shows how big the scatter in the data is.
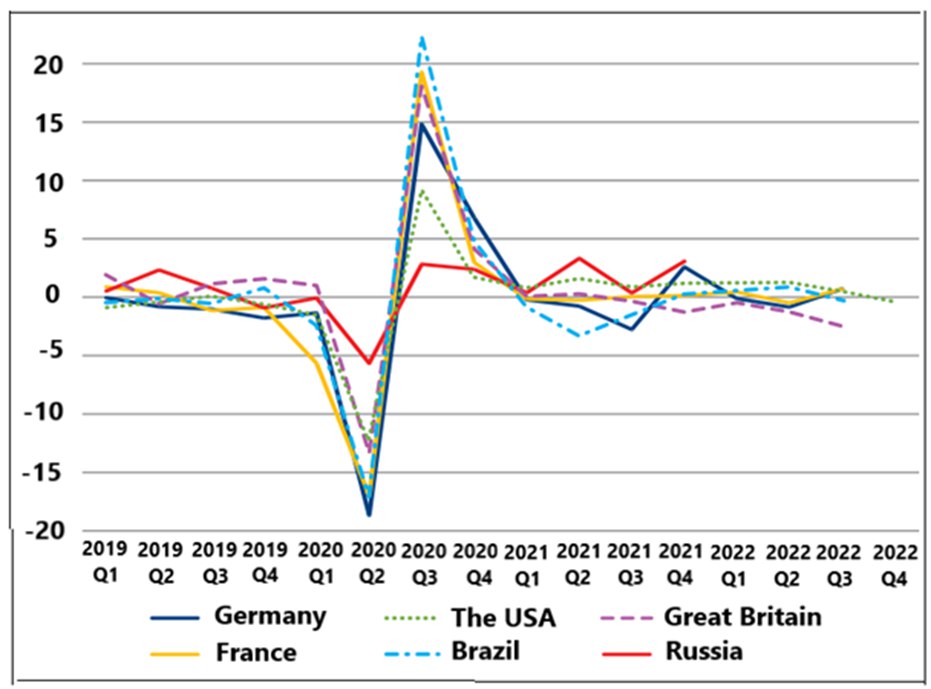
Dynamics of the industrial cycles of the world economy in 2019-2022, calculated using this model
It is believed that at a normal distribution all the forecast data will fall within the limit from -3 to +3 sigma – six sigma in total. In this case it is possible to forecast 99.75% of events. In practice, all that falls beyond the six sigma – are abnormal processes.
However, applied mathematics always strives to improve the result. In the calculations by Sergei Aliukov, if suspiciously many points accumulate in the borderline zone (for instance between 2 and 3 sigma) and a trend for some anomaly is identified, one could use the limit of not six but eight sigma and thus improve the accuracy of the forecast.
The paper words the main provisions of the macroeconomic theory, which is based on “quickly changing” processes. At the same time it becomes possible to forecast the macroeconomic jumps. The elaborated theory is illustrated by a number of practical examples, including examples from the economy of Russia.
The paper by Sergei Aliukov has been published early in 2024, but it has already sparked great interest among the scientific community. Professor Aliukov has received a letter from India with an offer to include his method in the new edition of the Premier-archive of Applied Mathematics, a selected multivolume collection of the world’s best papers on this topic.
In addition, this paper will be included in the selected papers of the Mathematics journal of the MDPI publishing house, compiled of the works by the SUSU academic staff members.
The new approach to forecasting the macroeconomic growth proposed by the SUSU professor, Sergei Aliukov, has been developed to a level of concept for now. It needs further elaboration and testing, but it will definitely be noticed by the world of applied mathematics.




